Demo computing and displaying the uncertainty regions
Contents
Loading
Take account of all folders and subfolders of code
init; % Load the image and the data associated to the files img_1344.* d=DatasetLoaderToulouse(); imgData = d.getImageDataAtImageName('img_1344'); % Load the polygons of the uncertainty regions polys = imgData.polys; % Merge the polygons mergedPolys = {[],[],[]}; for i=1:3 mergedPolys{i} = mergePolygons(polys{i}); end
The variable mergedPolys is an cell with the three polygons of the uncertainty regions associated to the three vanishing points. However, theses polygons may be cut by the line at infinity reprented in homoneous coordinate as [0 ; 0 ; 1]. On a 2D projection on the image plane, these polygons would lie on the top and the bottom of the image and would join at infinity. It can be convenient to have the polygons cut by the line at infinity, ie a set of polygons, for example for 2D projection on the image plane. The variable polys provide three sets of polygons (sepatated by the ilne at infinity). Each set of polygons can be merged to get the polygons from mergedPolys.
Compute the uncertainty regions
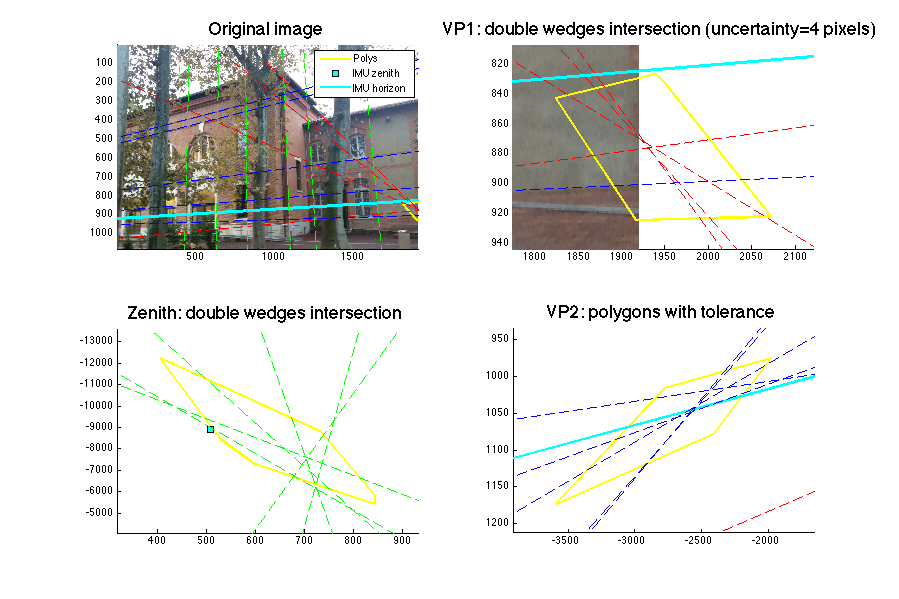
Compute the intersections of the double wedges generated from the three classes of segments. We use an uncertainty of 4 pixels.
polyEstimator = PolyEstimator(); [polys, mergedPolys, maxNoise] = polyEstimator.compute_polys(imgData, 4); color = ['r', 'g', 'b']; width = size(imgData.img, 2); height = size(imgData.img, 1); % Compute the zenith and the horizon from the IMU data zenith = imgData.K * imgData.R_imu * [0 ; 0 ; -1]; zenith = zenith / zenith(3); horizon = imgData.Kinv' * imgData.R_imu * [0 ; 0 ; -1];
Plots in the image space
% Store the axes of the 4 subplots in order to simulateneouly draw in the 4 subplots figure('position', [0, 0, 900, 600]); axes = []; for i=1:4 axes(i) = subplot(2, 2, i); end % "Hold on" on the 4 subplots mhold(axes, 'on'); % Display the image in the 4 subplots mimagesc(axes, imgData.img); % Draw the polygons polygonsLines = []; for i=1:3 if length(polys{i}) < 1 continue; end % Compute the best axis polyAxis = bestPolygonsAxis([Inf -Inf Inf -Inf], polys{i}); dx = polyAxis(2) - polyAxis(1); dy = polyAxis(4) - polyAxis(3); polyAxis(1) = polyAxis(1) - dx/5; polyAxis(2) = polyAxis(2) + dx/5; polyAxis(3) = polyAxis(3) - dy/5; polyAxis(4) = polyAxis(4) + dy/5; axis(axes(i+1), polyAxis); % Concatenate the line segments of the polygons in the same polygonsLines matrix for iPoly=1:size(polys{i},2) poly = infinitePolygonAxisFit(polys{i}{iPoly}, polyAxis); poly = poly([1:end,1],:); % Repeat last vertex polygonsLines = [polygonsLines poly(:,1:2)' [NaN ; NaN]]; end end mline(axes, 'XData', polygonsLines(1,:), 'YData',polygonsLines(2,:), 'color', 'y', 'LineWidth',2); % Plot the zenith and the horizon mplot(axes, zenith(1), zenith(2), 's', 'LineWidth',1, 'MarkerEdgeColor','k', 'MarkerFaceColor', 'c', 'MarkerSize',6); mhline(axes, horizon, 'color', 'c', 'LineWidth',2); % Display all the gt lines for i=1:size(imgData.lines,1) mhline(axes, cross([imgData.lines(i,1:2) 1]', [imgData.lines(i,3:4) 1]'), 'LineStyle', '--', 'Color', color(imgData.vp_association(i))); end % Set the legend, title and axis legend(axes(1), {'Polys', 'IMU zenith', 'IMU horizon'}); t = title(axes(1), 'Original image'); set(t, 'FontSize', 18); t = title(axes(2), sprintf('VP1: double wedges intersection (uncertainty=%d pixels)', maxNoise)); set(t, 'FontSize', 18); t = title(axes(3), 'Zenith: double wedges intersection'); set(t, 'FontSize', 18); t = title(axes(4), 'VP2: polygons with tolerance'); set(t, 'FontSize', 18); for i=1:4 axis(axes(i), 'ij'); end axis(axes(1), [1 width 1 height]); mhold(axes, 'off');
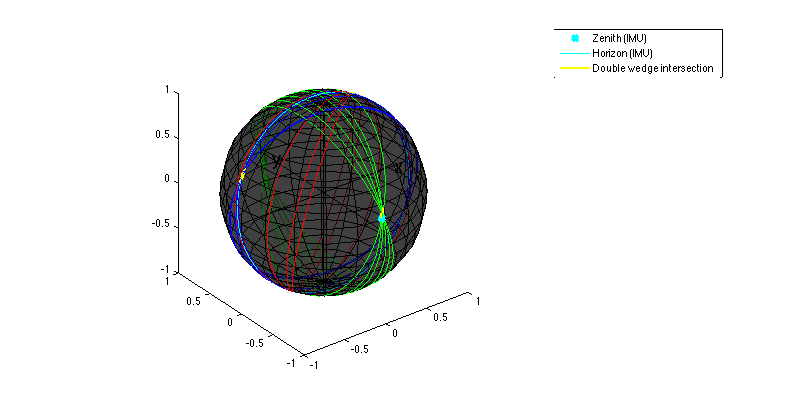
Plot in the Gaussian sphere
figure('position', [0, 0, 800, 400]); xlim([-1 1]);ylim([-1 1]);zlim([-1 1]); set(gca,'drawmode','fast'); hold on % Draw the unit sphere drawSphere('k'); % Draw the lines for i=1:size(imgData.lines,1) if imgData.vp_association(i) == -1 continue end plotCircle3D([0 0 0], (imgData.K' * imgData.linesEq(i,:)')', 1, color(imgData.vp_association(i))); end % Draw the horizon and the zenith phorizon = plotCircle3D([0 0 0], (imgData.K' * horizon)', 1, 'c'); gszenith = imgData.Kinv * zenith; gszenith = gszenith/norm(gszenith); pzenith = plot3(gszenith(1), gszenith(2), gszenith(3), 'xc', 'LineWidth',3); % Draw the intersections of the double wedges for i=1:3 mergedPoly = mergedPolys(i); gspoly = imgData.Kinv * mergedPoly{1}'; gspoly = gspoly ./(ones(3,1)*sqrt(sum(gspoly.*gspoly, 1))); pPoly = plot3(gspoly(1,[1:end 1]), gspoly(2,[1:end 1]), gspoly(3,[1:end 1]), 'y', 'LineWidth',2); end hold off % Set the title and the legend t = title(axes(4), 'Gaussian sphere representation'); set(t, 'FontSize', 18); legend(gca, [pzenith, phorizon, pPoly], 'Zenith (IMU)', 'Horizon (IMU)', 'Double wedge intersection');